2. Types of DGGS

Five design considerations of a DGGS

There are different DGGS implementations based on different design considerations. Sahr, White, and Kimerling (2003) catalogued those considerations into five aspects to specify a DGGS. Those aspects are:

1. Base polyhedron
2. Polyhedron orientation
3. Refinement
4. Projection
5. Assigning points to zones

We simplify it further by focusing on only three aspects (Base polyhedron, Refinement and Projection) to compare the three DGGS implementations in the following table:

	IGEO7	H3	HEALPix	rHEALPix
Base polyhedron	Icosahedron	Icosahedron	Sphere*	Cube
Refinement	hexagonal refinement ratio 7	hexagonal refinement ratio 7	square* refinement ratio 4	mixed shape refinement ration 9(4*)
Projection	Icosahedral Snyder Equal Area	gnomonic	HEALPix Spherical Projection	rHEALPix projections
Features	Uniform neighbours Equal area Sphereical	Uniform neighbours Non equal area Sphereical	isoLatitude Equal area Sphereical	isoLatitude Equal area Ellipsoid

IGEO7

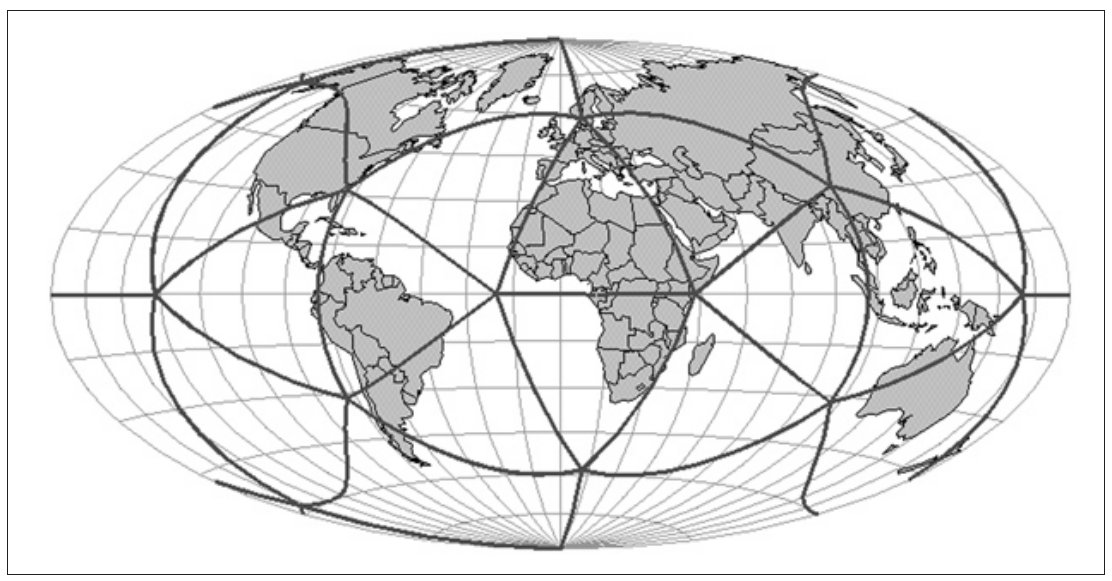
IGEO7 is implemented in the tool DGGRID and was described at the AGILE 2025 conference (2025). It is also a hexagonal DGGS based on a icosahedron with a refinement ratio of 7, similr to to H3. However, it uses the Icosahedral Snyder Equal Area (ISEA) as its projection to achieve equal area for all zones at the same refinement level. The following figure shows how the 20 faces of icosahedron are oriented and tiled.

IGEO7 orientation - Sahr et al. (2003)

Zone ID and indexing

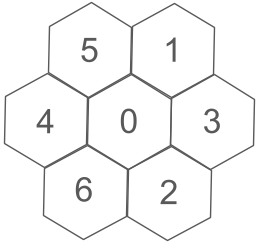
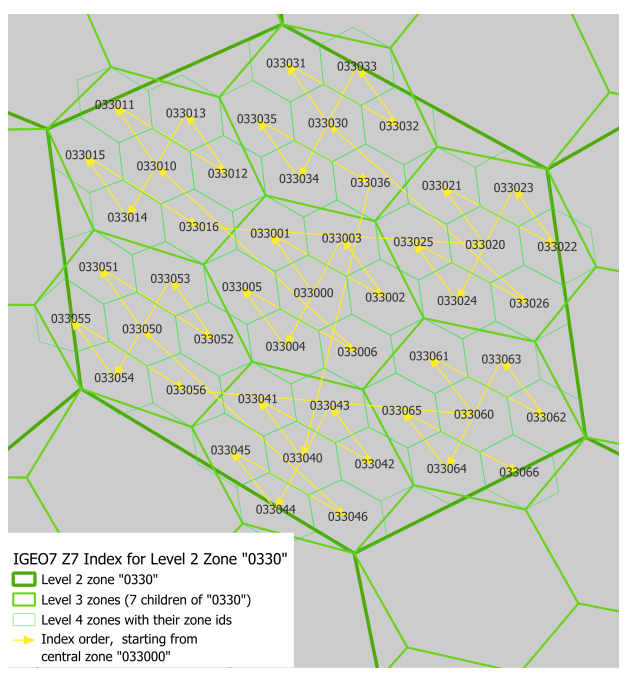
The zone ID of IGEO7 formation is similar to rHEALPix; it is a string of digits (e.g.00142352345) where the first two digits are the face ID. Each digit after the face ID represents the child zone position of the parent. The child zone is ordered according to the Central Place Indexing (CPI) hierarchy index introduced by Sahr (2019). The following figure shows how child zones are ordered to create the zone ID at each level.

IGEO7 zones ordering

IGEO7 zones traversal - Kmoch et al. (2025)

Zone area distortion

The zone area distortion is very small. The are twelve pentagons (vertices of icosahedron) at every resolution. To reduce the effect of those regions, the orientation of the icosahedron is carefully designed so that most of them fall into the ocean.

IGEO7 global area distortion - Kmoch et al. (2022)

H3

H3 is the first commercial hexagonal DGGS developed by Uber for spatial event-driven data analysis. It follows the Dymaxion orientation to unfold the icosahedron into 20 tiles. The 20 tiles are subdivided into hexagons with a refinement ratio of 7. Those hexagons are inverse projected back to the sphere using gnomonic projection.

H3 Dymaxion orientation (Wiki)

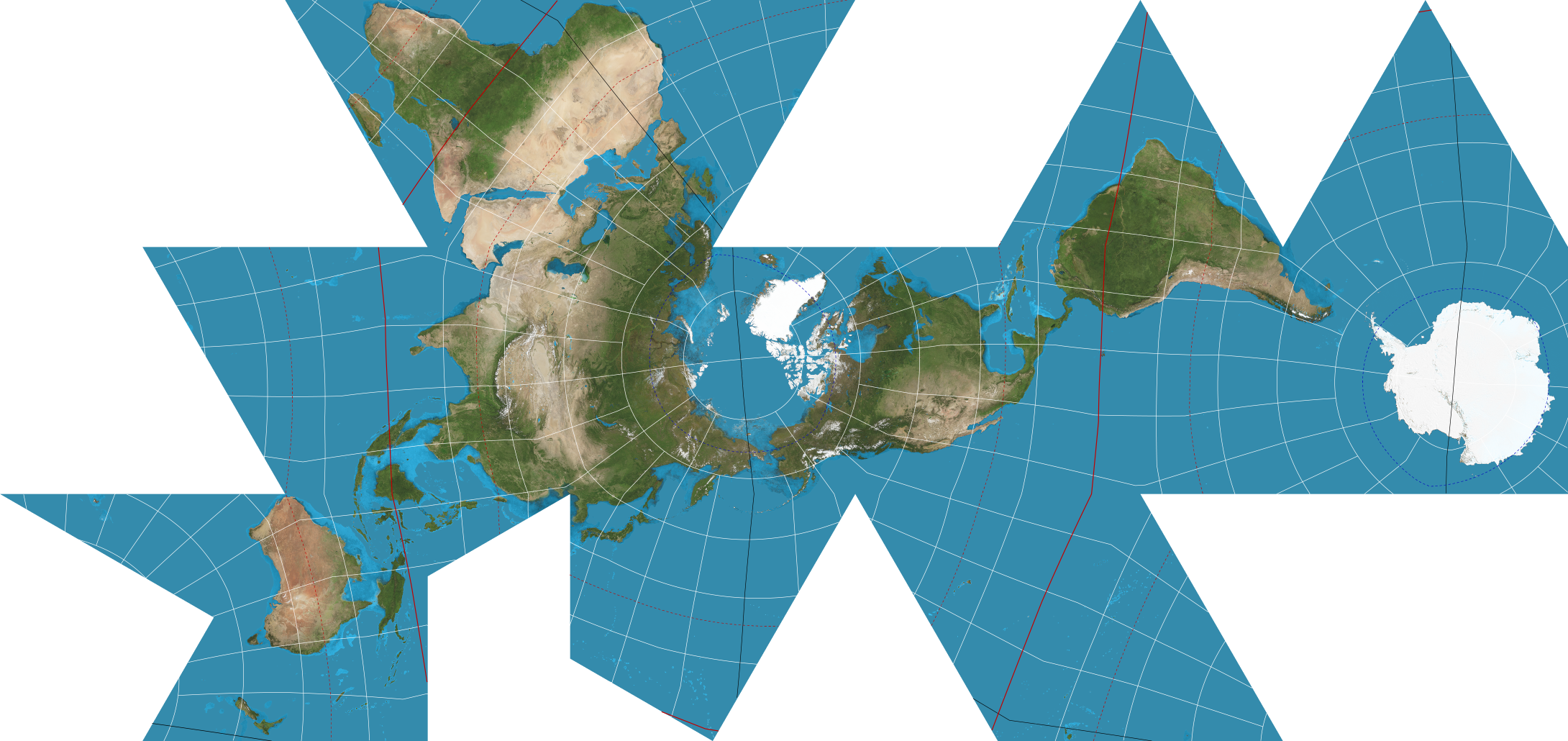
Zone ID and indexing

The zone ID of H3 is a 64-bit integer, but the canonical hexadecimal representation of the integer is commonly used instead. According to the H3 documentations, the zone ID are similar to IGEO7 follows CPI schema.

Zone area distortion

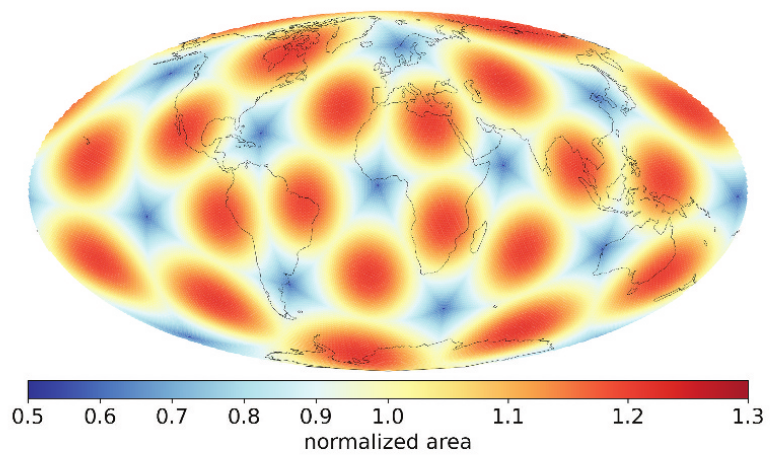
The zones of H3 are not equal in area over the globe at the same refinement level. For example, the web toolkit from the H3 web shows that the zone area from Greenland differs from Australia’s, with 200 km².

Alexander Kmoch et al. (2022) shows the global area distortion for H3. The figure shows that the zone area varies in different regions over the globe.

H3 global area distortion - Kmoch et al. (2022)

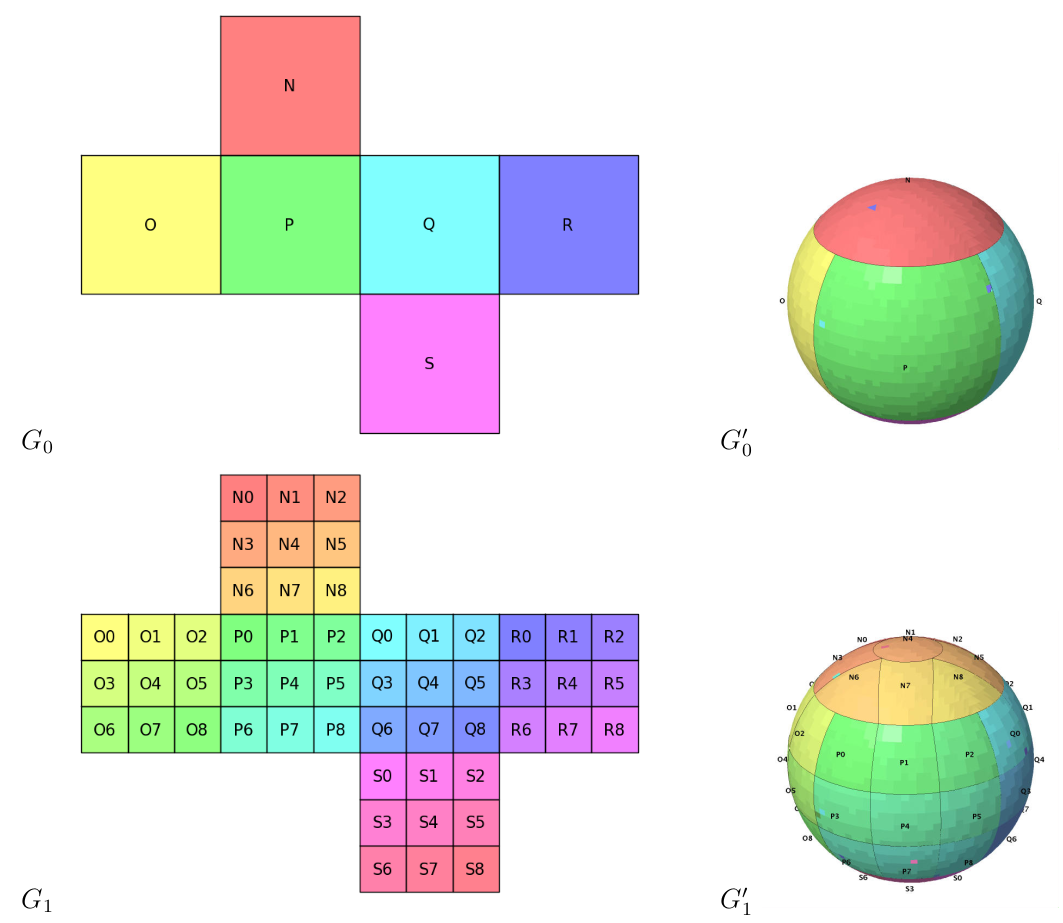
HEALPix

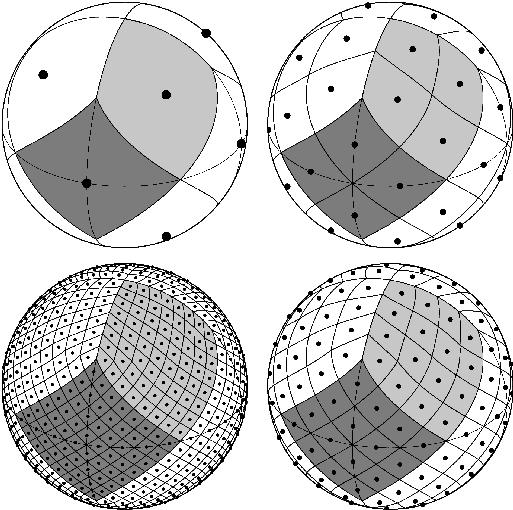
HEALPix(2005) originates from the astronomical community, and it is a hierarchical, congruent and aligned square grid projected to a sphere used to study the background radiation and global warming. HEALPix works directly on a sphere and pixelises (discretises in DGGS) the sky (Earth surface) into a map. It performs the partition directly on the sphere with the 12 pixels as the base. The following figure shows how the sphere is tessellated into finer refinement levels.

How HEALPix partition the sphere - Gorski et al. (2005)

Zone ID and indexing

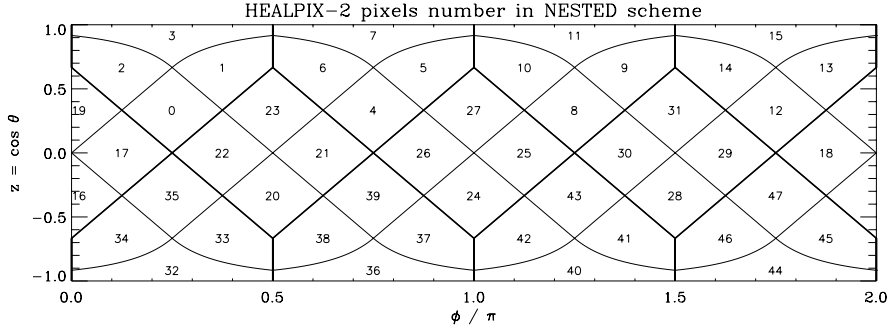
HEALPix has two indexing schemas: ring indexing and nested indexing. The ring index used the property of isolatitude to order the zones. Here, we will focus on the nested index that provides the hierarchical structure. The nested index uses QuadCube and follows the z-order space-filling curve, as shown in the following diagram.

HEALPix nested indexing - Gorski et al. (2005)

rHealpix

rHEALPix(2016) is a modification of the HEALPix projection from spherical to ellipsoids of revolution. Following the refinement schema, it projects an ellipsoid onto the cube and subdivides it into square grids. Then the grid is inverse projected back to the ellipsoids by the rHealpix projection. The following diagram shows how rHEALPix flattens the Earth into a cube of 6 tiles.

How rHEALPix tiles the globe - Gibb et al. (2016)

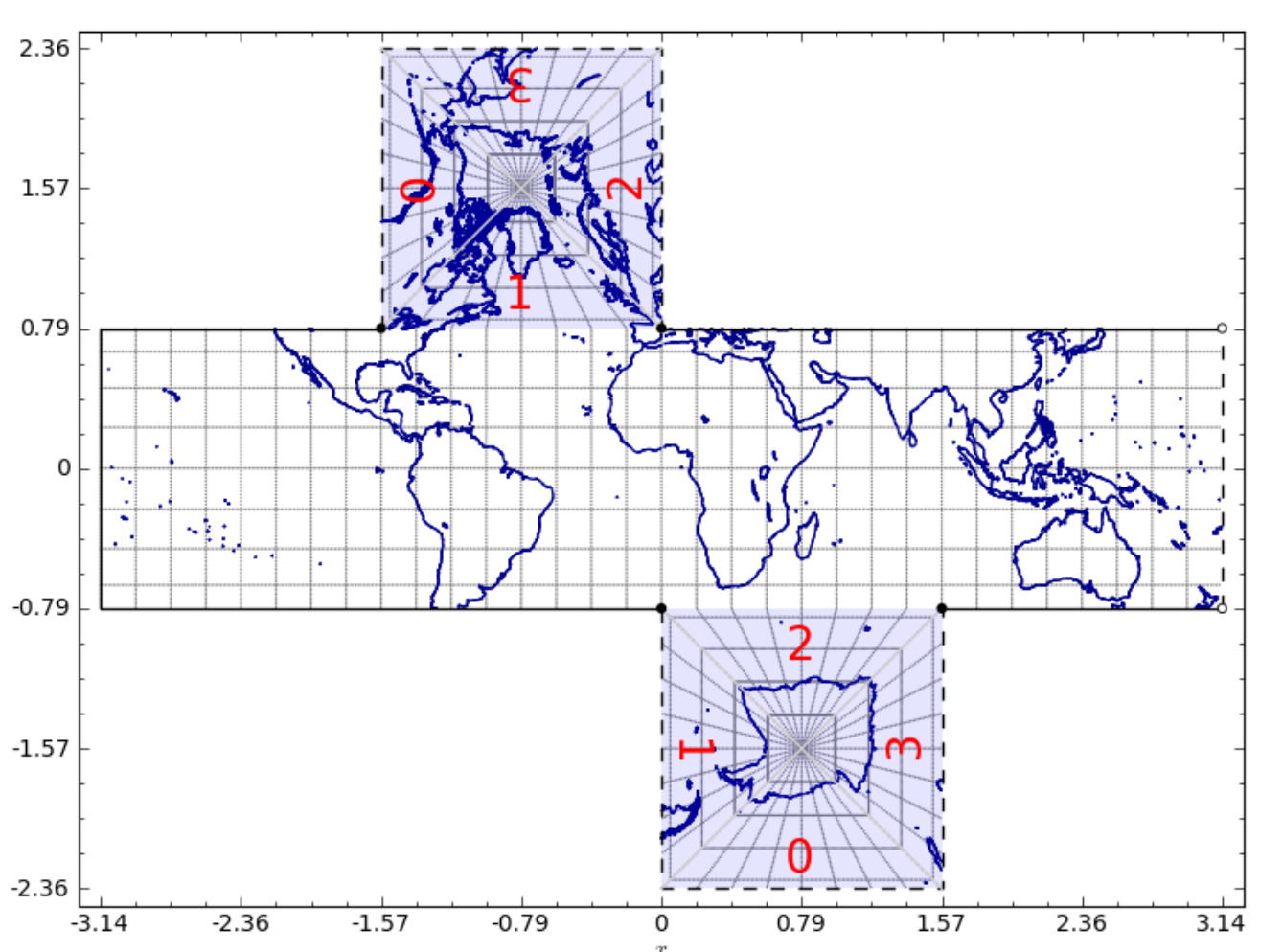
Zone ID and indexing

The following diagram shows how the planar square grid is inversely projected to an ellipsoid and how zones are indexed. The diagram G’1 shows the unique feature of rHEALPix - isolatitude. It is easy to see that all zone centroids align to the same latitude, and it is an important feature when performing spherical harmonic analysis.

rHEALPix projection - Gibb et al. (2016)

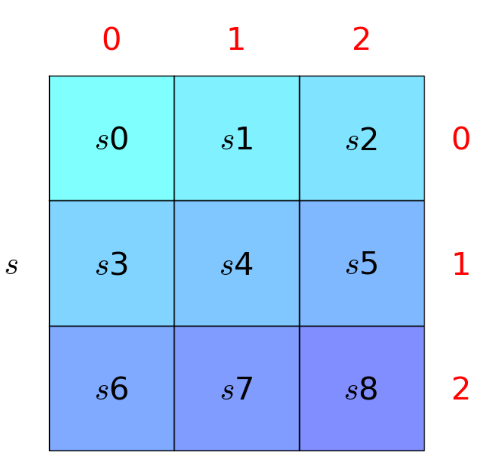
The zone ID of rHEALPix forms with a character that represents the faces of the cube, followed by a string of digits (e.g. P0212423). Each digit represents the discrete position of the subdivided square grid at the current refinement level. So the length of the digits shows the level of refinement. The digits are arranged according to the Z space-filling curve from top to bottom and left to right.

rHEALPix zone indexing - Gibb et al. (2016)

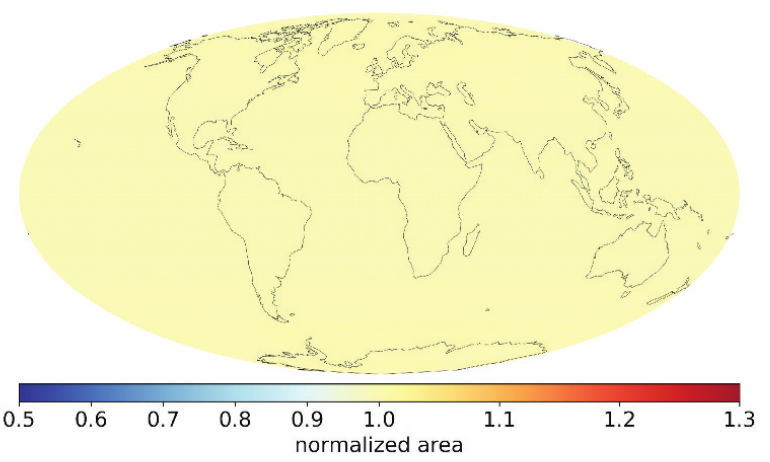
Zone area distortion

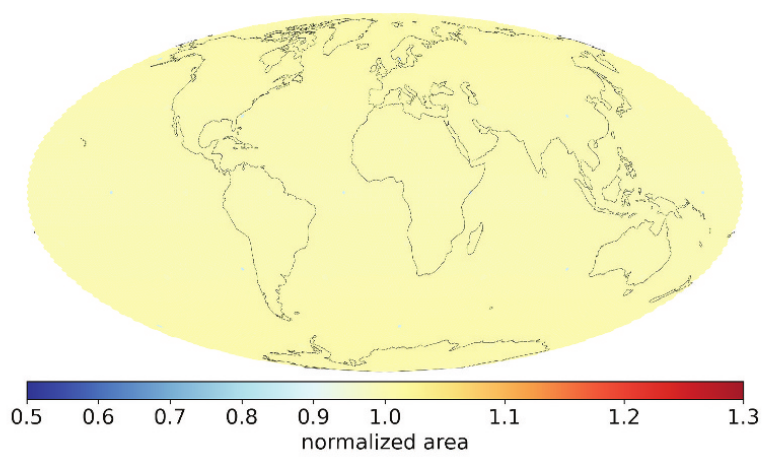
The HEALPix and rHEALPix projections are equal area for the globe at the same refinement level. Alexander Kmoch et al. (2022) studied the global area distortion of rHealpix. The following figure shows that the distortion is minimal and almost equal to the normalised area everywhere on the Earth.

rHEALPix area distortion - Kmoch et al. (2022)

Other DGGS

Other types of DGGS are available for different application needs (non-exhaustive list):

• DGGAL, the Discrete Global Grid Abstraction Library by Ecere implements several DGGS
• Uber H3, a widely used non-equal are hexagonal grid systems
• Google S2 provides a very efficient square grid for computation
• OpenEAGGR by RiskAware provides the triangle and hexagonal grids with a refinement ratio of 3 and 4, respectively
• Awesome Discrete Global Grid Systems (DGGS) - A collection of DGGS resources, listing many libraries that implement DGGS.

Several more are described in the scientific literature, but lack real-world implementations.

Gibb, Robert, A Raichev, and M Speth. 2016. “The rHEALPix DGGS.” https://doi.org/DOI:10.1088/1755-1315/34/1/012012.

Górski, K. M., E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, and M. Bartelmann. 2005. “HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere.” The Astrophysical Journal 622 (2): 759. https://doi.org/10.1086/427976.

Kmoch, Alexander, Ivan Vasilyev, Holger Virro, and Evelyn Uuemaa. 2022. “Area and Shape Distortions in Open-Source Discrete Global Grid Systems.” Big Earth Data 6 (3): 256–75. https://doi.org/10.1080/20964471.2022.2094926.

Kmoch, A., K. Sahr, W. T. Chan, and E. Uuemaa. 2025. “IGEO7: A New Hierarchically Indexed Hexagonal Equal-Area Discrete Global Grid System.” AGILE: GIScience Series 6: 32. https://doi.org/10.5194/agile-giss-6-32-2025.

Sahr, Kevin. 2019. “Central Place Indexing: Hierarchical Linear Indexing Systems for Mixed-Aperture Hexagonal Discrete Global Grid Systems.” Cartographica: The International Journal for Geographic Information and Geovisualization 54 (1): 16–29. https://doi.org/10.3138/cart.54.1.2018-0022.

Sahr, Kevin, Denis White, and A. Jon Kimerling. 2003. “Geodesic Discrete Global Grid Systems.” Cartography and Geographic Information Science. https://doi.org/10.1559/152304003100011090.